Menyatakan perkalian bilangan bulat berulang sebagai bilangan berpangkat

 

DEFINISI BILANGAN BERPANGKAT

bilangan berpangkat yaitu yakni bilangan yang dikalikan dengan dirinya sendiri hingga beberapa tingkat. Notasi pangkat digunakan untuk menuliskan berapa kali suatu bilangan dikalikan secara berulang dalam bentuk yang lebih sederhana.

Misalnya, kita memiliki faktor a yang dikalikan berulang sebanyak tiga kali, maka dapat ditulis:

a3 = a x a x a

Angka 3 dituliskan di sebelah kanan atas a, yang menunjukkan bahwa angka 3 ini merupakan pangkat dari a.

Contohnya, 23 = 2 x 2 x 2 = 8.

1. Pangkat Penjumlahan

Jika ada perkalian eksponen dengan basis yang sama, maka pangkatnya harus ditambah. Bisa dituliskan sebagai berikut:

am x an = am + n

Contoh: 24 x 22 = 24 + 2 = 26 = 64

 

2. Pangkat Pengurangan

Jika ada pembagian eksponen dengan basis yang sama, maka pangkatnya harus dikurang. Bisa dituliskan sebagai berikut:

am : an = am – n

Contoh: 25 : 23 = 25 – 3 = 22 = 4

 

3. Pangkat Perkalian

Jika ada bilangan berpangkat yang dipangkatkan lagi, maka pangkatnya harus dikali. Bisa dituliskan sebagai berikut:

(am)n = am x n

Contoh: (22)3 = 22 x 3 = 26 = 64

 

4. Perkalian Bilangan yang Dipangkatkan

Jika ada perkalian bilangan yang dipangkatkan, maka masing-masing bilangan tersebut dipangkatkan juga. Bisa dituliskan sebagai berikut:

(a . b)m = am . bm

Contoh: (2 x 3)2 = 22 x 32 = 4 x 9 = 36

5. Perpangkatan pada Bilangan Pecahan

Jika ada bilangan pecahan yang dipangkatkan, maka bilangan pembilang dan penyebutnya harus dipangkatkan semua, dengan syarat b ≠ 0, artinya penyebutnya tidak boleh sama dengan 0. Bisa dituliskan sebagai berikut:

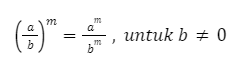
Contoh: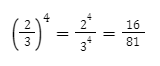 

 

6. Pangkat Negatif

Jika ada bilangan berpangkat negatif, maka nilainya sama dengan 1 per bilangan eksponen tersebut namun pangkatnya menjadi positif. Bisa dituliskan sebagai berikut:

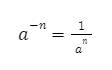
Contoh: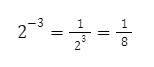 

 

7. Pangkat Pecahan

Jika ada bilangan berpangkat yang diakar, maka pangkat dari akarnya dapat ditulis menjadi penyebut dari pangkat bilangannya. Bisa dituliskan sebagai berikut:

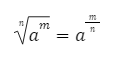
Contoh: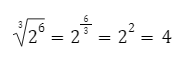 

 

8. Pangkat Nol

Jika ada bilangan yang berpangkat nol, maka hasilnya sama dengan 1 berapapun nilai bilangan basisnya, dengan syarat bilangan basisnya tidak sama dengan 0 (a ≠ 0). Bisa dituliskan sebagai berikut:

a0 = 1, untuk a ≠ 0

Contoh: 

• 20 = 1
• 70 = 1

• Contoh Soal Eksponen

1. Hasil dari 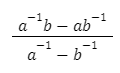 adalah….

Penyelesaian:

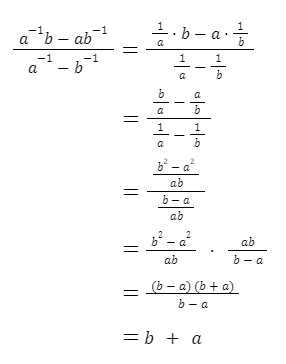
Jadi hasil dari 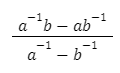 adalah b + a.

 2. Hasil dari y3 x 2 y7 x (3y)² adalah....

penyelesaian :

y3 x 2y7 x (3y)2 = y3 x 2y7 x 9y2

=(2 x 9)y 3+7+2
=(2 x 9)y12
=18 y12

3. Hasil 3m3 x (mn)4 adalah....

penyelesaian :

3m3 x (mn)4 = 3m3 ´ m4n4
=3m3+ 4 n4
=3m7 n4

4. Hasil (2×3) x 3(x2 y2)3 x 5y4 adalah....

penyelesaian :

(2×3) x 3(x2 y 2 )3 x 5y4 = (2×3 ) x 3(x2x3 y 2×3 ) x 5y 4
=(2×3 )x 3(x6 y6 ) x 5y4
=(2×3 ) x 3x 6 x y6 x 5 y4
=(2 x 3 x 5) x3+6 y 6+4
=30×9 y10

5. Hasil y3 x 2 y7 x (3y)² adalah....

penyelesaian :

y3 x 2y7 x (3y)2 = y3 x 2y7 x 9y2
=(2 x 9)y 3+7+2
=(2 x 9)y12
=18 y12